进才中学2019届高中三年级暑期作业测试数学考试试题
1、填空题
1.复数![]() 的虚部为_____________.
的虚部为_____________.
2.设集合![]() 则
则![]() ___________.
___________.
3.![]() 的展开式中
的展开式中![]() 的系数为________.
的系数为________.
4.过点M且和双曲线![]() 有相同的渐近线的双曲线方程为_________.
有相同的渐近线的双曲线方程为_________.
5.F是抛物线![]() 的焦点,定点A),若点P在抛物线上运动,那样
的焦点,定点A),若点P在抛物线上运动,那样![]() 的最小值为____________.
的最小值为____________.
6.若![]() ,架构方程
,架构方程![]() ,则该方程表示的曲线为落在矩形地区
,则该方程表示的曲线为落在矩形地区![]() 内的椭圆的概率是_________.
内的椭圆的概率是_________.
7.已知某三棱锥的三视图所示,则该三棱锥的体积为_________.
8.等比数列![]() 的前
的前![]() 项和为
项和为![]() ,若对于任意的正整数
,若对于任意的正整数![]() ,均有
,均有![]() 成立,则公比
成立,则公比![]() __________.
__________.
9.已知函数![]() ,则“
,则“![]() ”是“
”是“![]() 的最小值与
的最小值与![]() 的最小值相等”的_____
的最小值相等”的_____
条件.
10.已知![]() 是概念在R上的偶函,且在区间
是概念在R上的偶函,且在区间![]() 上单调递增,若实数
上单调递增,若实数![]() 满足:
满足:
![]() ,则
,则![]() 的取值围是___________.
的取值围是___________.
11.已知函数 ,其中
,其中![]() ,若存在实数
,若存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不一样的根,则
有三个不一样的根,则![]() 的取值范围是_______________.
的取值范围是_______________.
12.已知AB为单位圆上的弦,P为单位圆上的点,若![]() 的最小值为
的最小值为![]() ,当点P在单位圆上运动时,m的最大值为
,当点P在单位圆上运动时,m的最大值为![]() ,则
,则![]() 的值为________.
的值为________.
2、选择题
13.若![]() ,则
,则![]() 是
是![]() 的
的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件
14.若变量![]() 满足
满足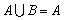 ,则
,则![]() 的最大值是
的最大值是
A.4 B.9 C.10 D.12
15.平面![]() 外有两条直线
外有两条直线![]() 和
和![]() ,若过
,若过![]() 和
和![]() 在平面
在平面![]() 内的射影分别是
内的射影分别是![]() 和
和![]() ,给出下列四个命题:①
,给出下列四个命题:①![]() ;②
;②![]() ;③
;③![]() 与
与![]() 相交
相交![]()
![]() 与
与![]() 相交或重合;④
相交或重合;④![]() 与
与![]() 平行
平行![]()
![]() 与
与![]() 平行或重合,其中不正确的命题个数是__________.
平行或重合,其中不正确的命题个数是__________.
A.1 B.2 C.3 D.4
16.已知两个不相等的实数![]() 满足以下关系式:
满足以下关系式:
![]() 则连接A
则连接A![]() 、B
、B![]() 两点的直线与圆心在原点的单位圆的地方关系是
两点的直线与圆心在原点的单位圆的地方关系是
A.相离 B.相切 C.相交 D.不可以确定
3、解答卷若![]() 求实数
求实数![]() 的取值范围;
的取值范围;
若![]() ,求实数
,求实数![]() 的取值范围。
的取值范围。
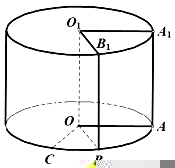
18.将边长为1的正方形![]() 绕
绕![]() 旋转一周形成圆柱,如图,弧AC长为
旋转一周形成圆柱,如图,弧AC长为![]() ,
,
弧![]() 长为
长为![]() ,其中
,其中![]() 与C在平面
与C在平面![]() 的同侧。
的同侧。
求圆柱的体积与侧面积;
求异面直线![]() 与OC所成的角的大小.
与OC所成的角的大小.
19.已知函数![]() ,若函数
,若函数![]() 的图像与函数
的图像与函数![]() 的图像关于
的图像关于![]() 轴对称。
轴对称。
求函数![]() 的分析式;
的分析式;
若存在![]() ,使等式
,使等式![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
20.设函数![]() .
.
若![]() ,解不等式
,解不等式![]() ;
;
若当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
设![]()
![]() 若存在
若存在![]() 使不等式
使不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
21.已知数列![]() 中,
中,![]() 又数列
又数列![]() 满足:
满足:![]() .
.
求证:数列![]() 是等比数列;
是等比数列;
若数列![]() 是单调递增数列,求实数
是单调递增数列,求实数![]() 的取值范围;
的取值范围;
若数列![]() 的各项皆为正数,
的各项皆为正数,![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,问:是不是存在整数
项和,问:是不是存在整数![]() ,使得数列
,使得数列![]() 是单调递减数列?若存在,求出整数
是单调递减数列?若存在,求出整数![]() ;若没有,请说明理由。
;若没有,请说明理由。






